Evaluation Approaches for Unlearning Algorithms
Efficiency
def. 언러닝 알고리즘 $ (\mathcal{U},C_\mathcal{U}) $의 efficiency이란 naive 제거 메커니즘 U*에 대한 제거 메커니즘 U의 상대적인 speed-up이다.

$h^{\mathcal{U}}=\mathcal{U}(\mathcal{A}(D),D,D_u)$ : unlearned model
$h^* = \mathcal{U^*}(\mathcal{A}(D), D, D_u)$ : naive retrained model
efficiency는 deletion 요청의 평균 값을 사용한다.
Effectiveness
def. $(\mathcal{U},C_\mathcal{U})$의 effectiveness란 naive 언러닝 모델의 테스트셋 성능과 비교한 언러닝 머신 모델의 테스트셋에 대한 성능이다.
effectiveness는 unlearned model의 테스트셋 성능과 naive retrained model의 테스트셋 성능을 비교하여 경험적으로 측정한다.
실제 값의 성능 metric $\mathcal{M}$가 주어졌을 때, 언러닝 알고리즘의 effectiveness를 측정하는 예시는 다음과 같이 두 quantities의 차이의 절댓값으로 표현될 수 있다.

- $ \mathcal{M}^*_{test}=\mathcal{M}(y^{pred}, y{test}) $
- $\mathcal{M^U_{test}}=\mathcal{M}(y^\mathcal{U}{pred}, y{test})$
effectivenss가 작을수록 unlearned 모델의 성능은 naive 모델의 성능과 가까워진다. 따라서 effectivenss가 작을수록 좋다.
Consistency
def. unlearned 모델과 naive 재학습 모델의 similarity를 평가
unlearned 모델이 naive 재학습 모델과 얼마나 비슷한지를 측정한다. exact unlearning 방법은 높은 수준의 consistency를 가짐을 보장한다. 효율성과 효율성과는 대조적으로, 우리가 고려하는 논문들은 일관성을 위한 여러 가지 measure들을 포함하고 있는데, 이 척도들은 그 사용법과 적용 가능성에 있어서 차이가 있다.
머신 언러닝 알고리즘이 parametric 모델에 적용될 경우에 consistency는 unlearned와 naive retrained 파라미터사이의 거리로 측정될 수 있다.

- $\theta^{\mathcal{U}}$ : $h^\mathcal{U}$의 파라미터
- $\theta^*$ : $h^*$의 파라미터
- $\lVert \cdot \rVert_2$: $l^2$ norm
consistency_\theta값은 작을 수록 좋고, 이는 unlearned 모델과 naive retrained 모델 파라미터가 비슷할수록 값이 작다.
He et al (2021)은 분류 모델에 적용되는 consistency 측정을 고려했다. consistency는 naive retrained와 unlearned 예측 사이에 일치하는 비율로 주어진다.

- 테스트셋은 $n_{test}$ 샘플만큼 포함되어있다.
- naive retrained 모델과 unlearned 모델의 예측이 비슷할 수록 consistency_y가 높게 계산되고, 이 값이 높을수록 좋다.
effectiveness와 certifiability가 높게 유지되는 경우 낮은 consistency가 허용될 수 있다. 이 경우 unlearned 모델의 정확한 예측은 다르지만 테스트셋에 대한 높은 성능은 유지된다. 특히 consistency는 이 상황에서 naive retrained 모델의 예측과의 차이를 나타내는 척도로 여전히 유용하지만 반드시 바람직하지 않은 머신 언러닝 알고리즘을 나타내는 것은 아니다. consistency 측정은 분류 모델로만 제한되지만 회귀 작업에 대한 유사점이 고려될 수 있다.
KL divergence(분산)는 두 확률분포 P와 Q의 유사성을 다음과 같이 측정한다.

KL 값이 작을수록 P와 Q의 유사도는 높아진다. 이를 이용하여 unlearned 모델 분포와 naive retrained 모델의 분포에 대한 KL분산을 측정함으로써 consistency를 측정할 수 있다. (회귀 모델에 사용하는 consistency)

consistency_{KL}는 값이 작을수록 좋다. 분류 작업에 적용될 경우, unlearned 모델과 naive retrained 모델 사이의 output 확률의 유사도를 측정하는데 KL분산을 이용한다.
Certifiability
def. removal 메커니즘 $\mathcal{U}$가 $D_u$를 unlearned 모델에서 제거된 능력을 평가
certifiability는 unlearned 모델이 삭제된 데이터에 해단 정보를 제거했으며, unlearned 요청이 규정을 준수하는지 여부를 보장한다. 이 중 중요한 부분은 삭제된 데이터에 대한 추론 공격에 대한 취약성을 정량화하고 최소화하는 것이며, 이는 외부 공격자가 삭제된 데이터를 식별하는 것을 포함한다. 잊힐 데이터 포인트의 영향을 제거하기 위해 exact unlearning 방법이 보장되지만, 여전히 삭제된 데이터 포인트를 기반으로 한 추론 공격에 취약할 수 있다. 이러한 경우, naive retrained 모델도 동일하게 이러한 추론 공격에 취약하다. 이러한 취약성을 최소화하기 위해 기울기 업데이터에 노이즈를 추가하는 등의 학습 절차를 변경해야 할수도 있다. 이전 섹션의 consistency는 certifiability의 선행 단계에 해당한다. certifiability에 대한 일부 정의와 측정값이 일관성을 보장하지 않으며, 더욱이 certifiability의 개념이 근본적인 수준의 consistency 개념에서 약간 제외되기 때문에 두 개념을 분리하기도 한다. consistency는 정확성 보장인 반면, certifiability는 보안 보장이다.
제거된 데이터 D_u에 대한 naive retrained 모델의 정확도는 모델이 이 데이터를 본적이 없는 제거된 데이터에 대해 가질 것으로 예상할 수 있는 정보의 양을 정량화한다. 예를 들어, 나머지 데이터에 유사한 데이터가 포함된 경우 이는 상당히 높을 수 있다. 따라서 이 정확도는 Mahadevan and Mathioudakis (2021)에서 수행된 것처럼 D_u에 대한 학습되지 않은 모델의 정확도를 비교할 수 있는 기준선이다. 여기서, 우리는 이를 일반적인 성능 metirc $\mathcal{M}$로 확장한다. $\mathcal{M}^∗_u := \mathcal{M}(y^∗_u , y_u)$ 와 $\mathcal{M}^\mathcal{U}_u := \mathcal{M}(y^\mathcal{U}_u , y_u)$이 각각 naive retrained 모델과 unlearned 모델의 D_u에 대한 성능을 나타낸다고 하자. certifiability는 다음에 의해 측정된다.

위 식의 우항을 $\mathcal{M}^*_u$와 $\mathcal{M}^\mathcal{U}_u$ 에 대한symmetric absolute precentage error($\mathrm{SAPE}(\mathcal{M}^*_u, \mathcal{M}^\mathcal{U}_u)$)라고 한다. 여기서는 $\mathcal{M}^*_u=0\%$, $\mathcal{M}^\mathcal{U}_u=10\%$가 $\mathcal{M}^*_u=80\%$, $\mathcal{M}^\mathcal{U}_u=90\%$보다 더 심각한 정보 침해를 나타낼 수 있다는 직관에 따라, $\mathcal{M}^*_u$이 작을때 더 많은 분산을 패널티 주기 위해 사용된다.
cerifiability의 값이 크면 unlearned 모델에 삭제된 데이터에 대한 정보가 포함되어있으므로 이 측정값은 모델 간 또는 시간이 지남에 따라 단일 모델의 certifiability 저하를 나타낼 수 있다. 그러나 certifiability는 삭제된 셋에 따라 성능의 유사성만 측정하기 때문에 작은 값이 반드시 이론적 보장에서 볼 수 있는 것과 같은 높은 수준의 certifiability를 의미하는 것은 아니다. 예를 들어, naive retrained 모델이 D_u에 대한 예측 성능이 높고 certifiability이 작다면, D_u에 대한 예측 성공률은 원본, naive, unlearned의 세가지 모델 모두에서 유사하다. 이 경우 작은 certifiability는 unlearned 모델이 D_u가있는지 여부에 대해 높은 성능을 달성하기 때문에 데이터를 잊어버렸는지 여부를 구분하지 않는다. 이 문제를 해결하기 위해 He et al(2021)은 Sommer et al(2020)의 backdoor 검증 실험을 채택하고 적용한다. 이 실험에서 D_u는 증강되고 특정 대상 레이블은 이 증강 데이터와 연관되며, 이러한 데이터 및 해당 레이블은 backdoor 데이터라고 한다. 그 결과 모델이 D_u에 대해 훈련을 받은 경우에만 정확한 특정 backdoor 레이블을 예측할 가능성이 높다. 따라서 naive retrained 모델은 D_u에 대한 예측 성능이 좋지 않을 것으로 보장되며, 이를 통해 certifiability가 더 의미 있는 측정값이 될 수 있다.
Golatkar et al (2019)에서 Shannon Mutual 정보가 certifiability를 측정하는데 사용된다. 이는 두 랜덤 변수 X와 Y가 공유하는 정보의 양을 측정하고 다음으로 정의된다.

여기서 P_{Y|X}는 X에 대한 Y의 조건부 확률 분포이고, P_Y는 Y의 확률 분포다. 제거 부분 집합 D_u를 무작위 변수로 취급함으로써(예를 들어, 제거 지점의 무작위 선택을 통해), D_u와 unlearned 모델이 공유하는 상호 정보는 I(D_u;\mathcal{U}(\mathcal{A}(D), D, D_u))에 의해 주어진다. 이 상호 정보는 계산이 더 용이한 특정 KL-분산에 의해 위로부터 경계지어진다는 것이 나타난다. 특히, 일단 D_u가 선택되고 고정되면 consistency_{KL}은 상호 정보에 대한 경험적 상한을 제공한다. 이 절차는 일반적으로 적용되지는 않는다.
Exact Unlearning Algorithms
SISA
가장 널리 적용될 수 있는 방법
sharding, slicing 방법으로 알려진 학습 데이터셋 reorganization을 통해 특정 데이터셋을 제거하고 scratch부터 재학습하는데 필요한 시간을 줄여준다. 전체 SISA 알고리즘은 경사 하강법과 같은 방법을 통해 점진적으로 학습을 하는 머신 러닝 모델에 적용할 수 있다. 그러한 모델에 대한 손실함수는 strongly convex할 필요는 없고, Bourtoule et al(2021) 는 SISA를 다양한 아키텍처의 DNN에 적용하였다. slicing없이 SISA는 decision tree를 포함한 모든 머신러닝 모델에 적용할 수 있다.

학습 데이터를 S shards로 나누고 그 안에서 R slices로 나눈다. S개의 독립적인 모델들은 slice들로 인해 점차적으로 학습되고, 이 모델들의 prediction들을 합쳐서 최종 output을 만든다. unlearn할 데이터는 위 그림에서 빨간색으로 표시되어있다. 이 데이터 포인트를 unlearn하기 위해서 slice D2,2로부터 시작하는 과정의 M2만 재학습하면 된다. 알고리즘에서 M2 모델을 h2로 표시할 것이고 저장된 중간 모델 state $\tilde{h}_{2,j}$(1≤j≤R)은 slice j까지 반영되어 학습된 모델을 말한다.
- D1,1이랑 D2,1은 다른건가? shard는 무엇을 기준으로 나눈거고(어떤 것이 다른 것이고) slice는 무엇을 기준으로 나눈 것인지?
Methodology
Sharded
- 원래의 학습 데이터셋은 동일한 크기의 shards로 나누어지고 각 학습 데이터 포인트는 정확히 하나의 shard에 포함된다. 이는 학습 데이터 포인트들이 앙상블 모델을 만드는 많은 learners로 표현될 수 있다는 점에서 다른 앙상블 모델링 기술과 대조된다.
Isolation
- 각 shard는 하나의 shard의 데이터 포인트에만 영향을 주도록 다른 shards와 분리되어 학습된다.
Slicing
- shards는 slices로 다시 나뉘어 학습 단계에서 점차적으로 나타내어진다. 각 slice이후부터 학습된 모델 state가 저장된다.
Aggregation
- 데이터 포인트에 대한 최종 모델 예측을 형성하기 위해 각 sharded 모델의 예측값들을 합친다. 이때 다양한 방법들을 통해 합쳐질 수 있다.
특정 데이터 포인트에 대해 제거요청이 들어오면, 해당 데이터 포인트를 포함한 shard에서 학습된 모델만 해당 데이터 포인트를 포함하는 slice이후에서부터 재학습하면 된다. 그 결과 예상되는 재학습 시간은 naive 재학습보다 빠르게 된다. 사용되는 shard와 slice의 수에 따라 단축되는 시간이 달라진다. 알고리즘 1과 2는 학습과 unlearning 절차에 대한 알고리즘이고 삭제 요청의 분포에 대한 사전 지식(prior knowledge)이 없다고 가정했을 때는 shard와 slice를 랜덤하게 선택한다. 삭제 요청에 대한 분포의 사전 지식(prior knowledge)은 SISA 방법을 향상시킬 수 있고 이는 Machine Unlearning(2020) 논문에서 논의된다. 알고리즘 1,2에서 $\mathrm{TRAIN}(D|\tilde{h})$ 함수는 모델 상태 \tilde{h}를 초기화하고 데이터셋 D로 학습함으로써 모델을 생성한다.
inference 단계 동안 aggregating하는 다양한 방법이 사용될 수 있다. 단순한 라벨 기반의 다수결은 투표는 각 구성 모델이 앙상블 모델의 최종 결정에 동일하게 기여하는 것을 포함한다. 그외에도 클래스의 아웃풋 벡터나 각 모델의 연속적인 prediction을 평균내는 방법들이 있다. 후자의 방법은 단순한 데이터셋에 대해 정확도에 주목할만한 효과를 낸다고 밝혀진바 없지만 라벨 기반 다수결 투표보다는 벡터 평균내어 aggregation하는 것이 더 복잡한 ImageNet task에서 높은 정확도를 가진다고 한다.


DARE Forests
decision-tree에 적용되는 방법.
DaRE forest는 DaRE trees를 앙상블하는 방법이다. 이때 각 tree는 학습 데이터의 복사본으로 독립적으로 학습되고 이 부분은 전통적인 랜덤 포레스트의 boostrapping과는 다르다. 이 부분 외에도, DaRE forest 앙상블은 랜덤 포레스트와 동일한 방법의 앙상블이다, 특히 \tilde{p}의 랜덤 subset features는 각 split로 고려된다.
이 섹션의 나머지 부분에는 DaRE trees에 초점을 둘것이고, 알고리즘3의 DaRE 방법에서 처음으로?(initially) 학습되어야 한다. 보통 의사결정 나무에서 DaRE trees는 재귀적으로 대부분 노드에서 split 기준으로 최적화하는 특성과 threshold를 선택함으로써 학습된다. 이것들은 일반적인 의사결정 나무와 다음 3가지 주요 방법에서 다르다.
exact unlearning 알고리즘 보면 새로 제안된 방법이 아니라 매우 간단한 알고리즘, 심지어 기존에 있는 알고리즘을 약간 변형한 것에 지나지 않는 것 같다.
Approximate Unlearning Algorithms
Fisher
사전학습된 convex 모델의 파라미터를 시간 효율적인 방식으로 업데이트하는 근사 unlearning 알고리즘. 이 방법은 scratch부터 재학습하지 않고 특정 데이터에 대한 정보를 제거할 수 있다. Newton correction과 noise injection의 전략을 섞음으로써 이를 가능케 했다. 제거된 데이터에 대해 추출될 수 있는 정보 양의 정확한 상한 bound가 계산될 수 있다.
methodology
Golatkar et al(2019)는 배치 언러닝 제거 매커니즘을 구현했고 이로 인해 D의 subset은 파라미터를 가지는 학습된 모델로부터 언러닝된다. 그들은 unlearned 모델로부터 나온 outputs의 확률 분포와 naive하게 retrain된 모델 사이의 KL 발산이 0이 된다면, 정보를 잊는 것이 보장될 수 있다는 조건을 도입함으로써 “완전히” 잊음의 정의를 공식화했다. 해당 논문의 proposition 1에 의하면, 이는 또한 제거된 데이터 D_u와 언러닝된 모델 $U(h_\theta, D, D_u)$ 사이의 $I(D_u;U(h_\theta,D,D_u))=0$이 되는, 즉 Shannon Mutual 정보가 0인 경우를 보장한다고 한다. 저자들은 그러므로 KL 분산을 언러닝 목표 함수의 부분으로 최소화하는 것을 강조했다. 이는 남아있는 데이터에 대해 single Newton step을 통해 처음 모델의 파라미터를 업데이트 함으로써 혹은 이 Newton step의 방향으로 가우시안 노이즈를 추가함으로써 혹은 둘다 함으로써 얻어질 수 있다. 원래 모델의 가중치에 Newton correction와 noise injection하여 Fisher 학습과 언러닝 방법은 각각 다음으로 표현된다.

SGD가 확률적 경사 하강 알고리즘일때 \theta_{init}은 초기화된 파라미터이고, \theta^U는 언러닝 파라미터이다. \sigma는 noise 파라미터이고 0보다 크다. F는 Fisher 정보 행렬이고, b\sim N(0,I)^P는 가우시안 노이즈이고 p는 학습데이터의 차원이다.
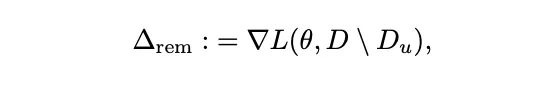
이는 남은 데이터에대해 \theta의 손실함수의 gradient를 의미한다. Fisher 정보 행렬은 Fisher 행렬이 계산하는데 비용이 많이 들기 때문에 Hessian으로 근사하여 사용된다. 몇몇 경우에, loss함수가 log-likelihood 일때 Fisher Information Matrix와 Hessian이 우연히 일치할때도 있다. 이 방법을 사용한 미니배치에서의 데이터 포인트 삭제에 대한 알고리즘은 알고리즘 5에 보여진다.

Performance
Efficiency
- 원본 논문 외에도 (2021)는 차원과 크기가 다양한 데이터 세트에서 피셔 방법의 성능을 평가한다. 그들은 Fisher 방법이 데이터 세트의 차원 범위(28~3072)와 크기(약 10^4~10^6)에 걸쳐 적당히 효율적인 언러닝 방법임을 보여준다. 노이즈 매개 변수인 σ = 1을 제어하고 하나의 미니 batch만 사용하여 이 방법이 저차원 데이터 세트의 경우 최대 50배의 효율성을 제공하는 반면 고차원 데이터 세트의 경우 약 1.8배에 불과하다는 것을 발견했다. 서로 다른 차원에서 알고리즘의 성능에 큰 차이가 있는 것은 역 Hessian 행렬을 계산하는 비용의 차이 때문이며, 이는 차원이 낮을 때 계산하는 것이 훨씬 빠르다.
Effectiveness
- (2019, 표 1)에서 Lacuna-10 및 CIFAR-10 데이터 세트에서 100개 이미지의 하위 집합을 학습하지 않을 때 Fisher 방법의 효과는 각 경우에 약 4~5%이며, 이는 유효성으로 측정된다. 이는 약 2~3%의 백분율 오차로 해석되며, 이는 (2021, 식(19))가 사용한 측정값으로, 테스트된 6개의 데이터 세트 모두에서 ≤ 1%의 백분율 오차를 달성다. (2021)에서 관찰된 더 나은 효과는 업데이트 단계에서 미니 배치를 사용한 결과다.
Consistency
- Consistency는 (3.5)의 KL-분산 측정 Consistency_{KL}에 대한 계산 가능한 상한을 제공함으로써 (2019, Proposition 2)에 제공된다. 이 한계는 Lacuna-10 데이터 세트의 경우 3.3이고 cifar-10의 경우 33.4이다.
(2019)에서 볼 수 있듯이 KL-분산 측정(3.5)은 Shannon Mutual 정보의 상한이다. 따라서 D_u와 언러닝 모델 사이의 Shannon Mutual Information은 Lacuna-10 데이터 세트의 경우 최대 3.3kNAT, CIFAR-10의 경우 최대 33.4kNAT이다.
'인공지능 > 다양한 인공지능' 카테고리의 다른 글
| An Introduction to Machine Unlearning 논문 리뷰 (1) (0) | 2024.04.11 |
|---|---|
| [강화학습] Markorv Decision Process (0) | 2024.01.21 |
| [Meta-Learning] Prototypical Networks for Few-shot Learning 논문 리뷰 (0) | 2023.08.24 |
| [Meta Learning] Siamese Neural Networks for One-shot Image Recognition 논문 리뷰 (2) | 2023.08.17 |
| [Meta-Learning] Meta-Learning in Neural Networks: A Survey 논문 리뷰 (0) | 2023.08.10 |